レンズ絞りによる回折効果
カメラのレンズ絞りを絞りすぎると、光の回折効果のために、かえってぼやけてしまうことはよく知られています。いったいどの程度ぼやけるものなのか、簡単な方法で見積もってみました。
1)1次元の話
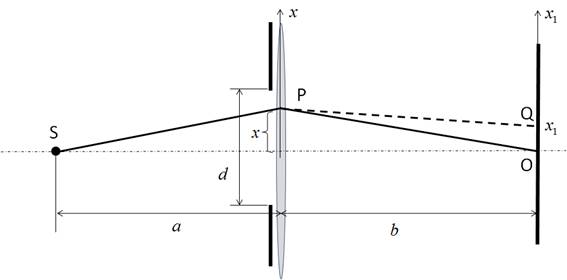
上の図のような光学系を考えます。絞りは本当は円形なのですが、ここではとりあえず1次元の話として、幅dのスリットを考えました。Sは点光源で、ここから出た単色の光はスリットを通過して、レンズによってスクリーン(撮像素子)上のO点に焦点を結ぶとします。
ここで、S点から出る1つの光線を考えることにします。また、レンズは極めて薄く、スリットと一体になっていると考えます。すると、光源から出た光はレンズ上のP点に到達し、ここでスリットによる光の回折現象によって、Q点にも光が到達すると考えます。光の通り道であるSPとPQの長さを求めてみます。レンズの中心から上向きにx軸をとり、P点の座標をxとします。同じようにスクリーン上でQ点の座標をx1とします。距離はそれぞれ
|
|
|
|
と求まります。光を波として考え、光源から波長λの単色光が放出されるとします。光の波が、S→P→Qと移動するときの位相変化に関係した項を、波の複素表示を用いて書くと、
|
|
|
(1) |
となります。ここで、![]() は波数で、波長を
は波数で、波長を![]() として
として![]() と表され、
と表され、![]() はレンズを通過することによる位相変化を表しています。
はレンズを通過することによる位相変化を表しています。
ちょうどO点に焦点を結ぶ時には、どの経路を通っても同じ位相になるはずなので、Cを距離の次元を持つ定数として、
|
|
|
(2) |
と表すことができます(厳密に言うと、光がO点に到達する場合とQ点に到達する場合で、経路がわずかだけ変化するので、![]() も変化するはずですが、O点とQ点は極めて近いとして、ここではそれを無視しています)。(2)式からL(x)は
も変化するはずですが、O点とQ点は極めて近いとして、ここではそれを無視しています)。(2)式からL(x)は
|
|
|
(3) |
になります。この関係を用いると、(1)式の{...}内は
|
|
|
(4) |
と変形することができます。ここで、スリットの幅は![]() に比べて十分小さいとして(
に比べて十分小さいとして(![]() )、
)、![]() という近似を用いました。
という近似を用いました。
(4)式を用いると、(1)式は次のように変形されます。
|
|
|
(5) |
Q点での光の振幅を![]() と表すことにします。Q点にはスリットの間にある、いろいろなxの値の点からの光が到達すると考えて積分を行うと、光の振幅は、
と表すことにします。Q点にはスリットの間にある、いろいろなxの値の点からの光が到達すると考えて積分を行うと、光の振幅は、
|
|
|
(6) |
と書くことができます。Q点での光強度を![]() とすると、
とすると、
|
|
|
(7) |
となります。最後の関数はsinc関数(![]() )の2乗を表し、1次元でのフラウンホーファ回折でお馴染みの式です。
)の2乗を表し、1次元でのフラウンホーファ回折でお馴染みの式です。
レンズの焦点距離をfとすると、次のレンズの公式が成り立ちます。
|
|
|
(8) |
この式と倍率![]() を用いると、
を用いると、
|
|
|
(9) |
という関係が得られます。この関係を用いると、最終的に
|
|
|
(10) |
という式が得られます。この式が、点光源から出た光がスクリーン上で焦点を結んだときに、光の回折効果により広がった像を表す式になります。
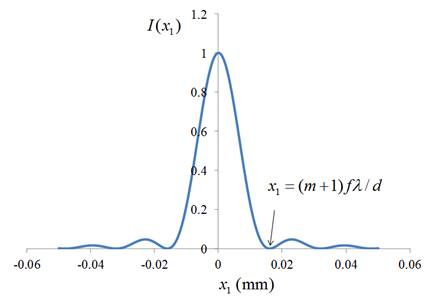
下の図は、焦点距離55
mmのレンズで、レンズのF値を16に合わせ、波長0.5 μmの光を放つ点光源を等倍で撮影した時のスクリーン(撮像素子)上での像を表しています。この時の実効F値は32になります。点光源を撮影したにも拘わらず、撮像素子上では点にならず、![]() を中心として幅をもったピークを与えます。
を中心として幅をもったピークを与えます。![]() 軸でこの像が初めて0になる点は
軸でこの像が初めて0になる点は![]() の条件で求められるので、
の条件で求められるので、![]() になります。この値は、ほぼ中央のピークの半値全幅の値に近いので、ぼやけの程度を表す量としてよく用いられます。つまり、ぼやけの幅を
になります。この値は、ほぼ中央のピークの半値全幅の値に近いので、ぼやけの程度を表す量としてよく用いられます。つまり、ぼやけの幅を![]() とすると、
とすると、
|
|
|
(11) |
となるわけです。ここで、![]() は実効F値です。無限遠方を撮影した時は、
は実効F値です。無限遠方を撮影した時は、![]() となるので、
となるので、![]() となり、平面波が入射したとき、レンズの焦点位置におけるスリットの回折像を与える式と一致します。
となり、平面波が入射したとき、レンズの焦点位置におけるスリットの回折像を与える式と一致します。
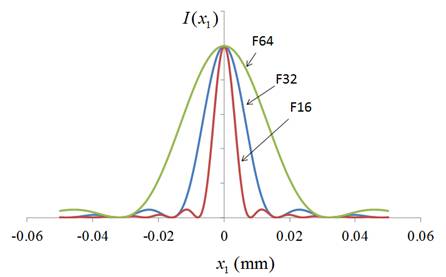
実効絞り値をいろいろと変化させて計算した結果を下図に示します。予想通り、絞りを絞っていけばいくほど像が広がっていくことが分かります。Nikon
D90では、ピクセルサイズが0.0055
mmなので、実効F値がF16のときは1.5ピクセル、F32の時は2.9ピクセル、F64の時は5.8ピクセルとなります。D90のときの空間分解能が、実測で3ピクセル、すなわち、0.0165 mm程度なので、実効F値が32程度になると影響が出始めることになります。
2)2次元の話
話はちょっとややこしくなりますが、2次元の場合も考えてみましょう。
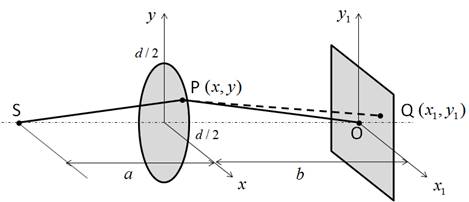
点光源Sから出た光は、円形の絞りとレンズがセットになった平面を通り、スクリーン上の点Oに焦点を結ぶとします。これを光線で考えてみます。Sから出た光は直径dの絞りで大きさを限られたレンズ上の点Pを到達します。絞りのために光は回折を起こし、スクリーン上の点Qに到達するとします。この時、SからPへ至る経路と、PからQへ至る経路の距離を計算してみましょう。
|
|
|
|
|
|
|
|
光がSからPを通りQへ到達したときの光の振幅の位相部分のみを書くと
|
|
|
(12) |
となります。ここで、![]() はレンズを通る時の位相変化です。スクリーン上で焦点を結ぶ経路に関しては位相因子は等しいことから、1次元の場合と同様にして
はレンズを通る時の位相変化です。スクリーン上で焦点を結ぶ経路に関しては位相因子は等しいことから、1次元の場合と同様にして![]() を求めると、
を求めると、
|
|
|
(13) |
となるので、Q点での光の振幅は、
|
|
|
(14) |
となります。直径dの絞りを通過するいろいろな経路での光の振幅を積分すると
|
|
|
(15) |
となります。ただし、Aは絞りの開口部を表し、光が通過できる範囲を表します。
この積分は絞りの内側の点の座標とスクリーン上の座標を、それぞれ次のような極座標で表すと分かりやすくなります。
|
|
|
(16) |
これらを(15)式に代入して、変数変換を行うと、
|
|
|
(17) |
となります。二重積分のうち、![]() に関する積分は次のベッセル関数を用いると簡単に表すことができます。
に関する積分は次のベッセル関数を用いると簡単に表すことができます。
ベッセル関数は積分表示で
|
|
|
(18) |
と定義されています。そこで、(17)式で![]() として
として![]() を
を![]() に変数変換し、また、
に変数変換し、また、![]() とおいて、(18)式と比べると
とおいて、(18)式と比べると
|
|
|
(19) |
となります。ただし、![]() とおきました。この式を(17)式に代入すると
とおきました。この式を(17)式に代入すると
|
|
|
(20) |
となります。さらに、ベッセル関数の性質![]() という関係式を用いると
という関係式を用いると
|
|
|
(21) |
と変形されます。
そこで、Q点での光強度を求めると、
|
|
|
(22) |
となり、2次元の円形開口による回折の結果と一致します。ここで、(9)式が成り立つので、![]() と倍率
と倍率![]() を使って表すと、最終的に
を使って表すと、最終的に
|
|
|
(23) |
という式に到達します。
1次元の場合と同じように、焦点距離55 mmのレンズで、レンズのF値を16に合わせ、波長0.5 μmの光を放つ点光源を等倍で撮影した時のスクリーン(撮像素子)上での像を計算してみます。この時の実効F値はやはり32です。
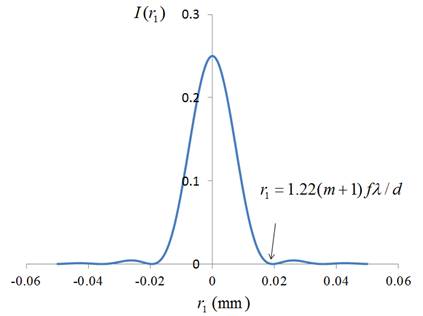
1次元の場合と似たグラフが得られました。ただし、このグラフでは原点をよぎる光強度分布を表すために、![]() を負の値を持つように拡張して書いてあります。1次元の場合と異なるのは、初めて0になる点が1.22の因子だけ大きくなっている点です。この値を用いて、ピークの幅、すなわち、ぼやけの幅を見積もると、
を負の値を持つように拡張して書いてあります。1次元の場合と異なるのは、初めて0になる点が1.22の因子だけ大きくなっている点です。この値を用いて、ピークの幅、すなわち、ぼやけの幅を見積もると、
|
|
|
(24) |
となり、1次元の時よりは1.22倍広くなっていることが分かります。ここで、![]() は実効F値です。
は実効F値です。